在找计算机相关的工作时,有一些基础是作为计算机学生必须了解的,总结如下
排序算法
归并排序
标准归并排序的实现,可以是通过递归,平均时间复杂度是O(nlogn),空间复杂度是O(n)
def mergeSort(nums, left, right):
if left >= right:
return nums
mid = left + (right - left) /2
mergeSort(nums, left, mid)
mergeSort(nums, mid + 1, right)
merge(nums, left, mid, right)
return nums
def merge(nums, left, mid, right):
i = left
j = mid +1
tmp = []
t = 0
while i <= mid and j <= right:
if nums[i] <= nums[j]:
tmp.append(nums[i])
i += 1
t += 1
else nums[i] > nums[j]:
tmp.append(nums[j])
j += 1
t += 1
while i <= mid:
tmp.append(nums[i])
t += 1
i += 1
while j <= right:
tmp.append(nums[j])
t += 1
j += 1
for kk in range(t):
nums[left + kk ] = tmp[kk]
面试的时候很喜欢问是否可以实现O(1)的空间复杂度,即不需要额外的空间。
原理如下,交换的时候,用的是翻转的特性:
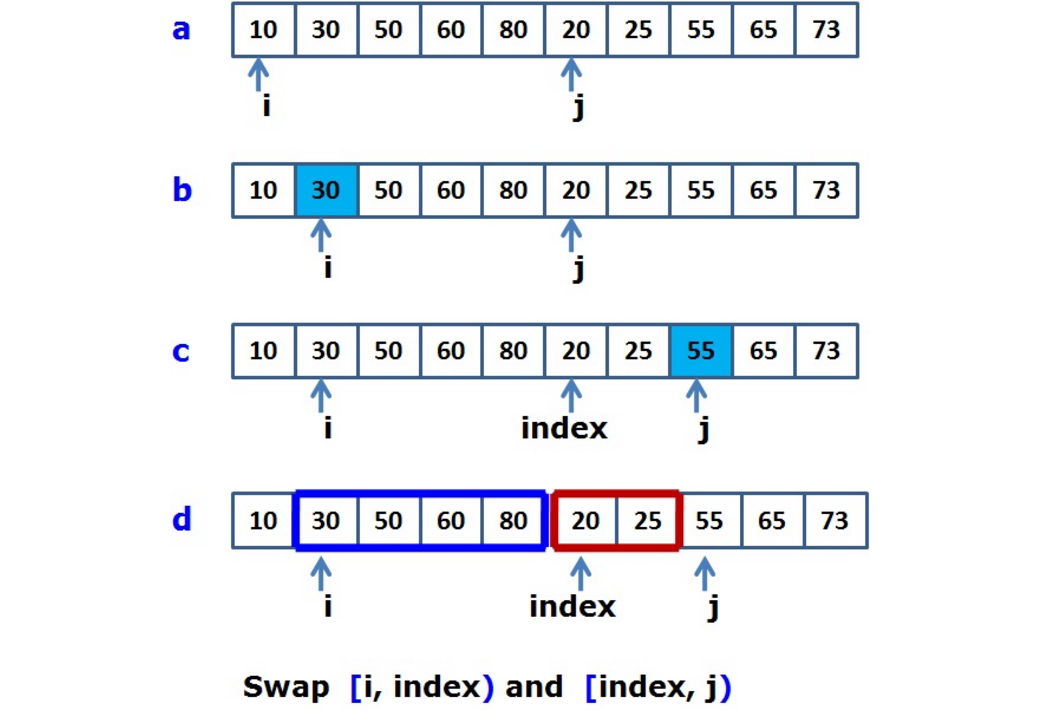
- i 往后移动,找到第一个arr[i]>arr[j]的索引。如图找到30
- j 往后移动,找到第一个arr[j]>arr[i]的索引。如图找到55
- 交换i到index-1和index到j的部分,采用局部数组循环移动的方法 通过三次数组逆序实现。交换后数组前半部分局部有序,之后重复进行此步骤即可实现两个有序数组的合并
def mergeSort(nums, left, right):
if left >= right:
return nums
mid = left + (right - left) / 2
mergeSort(nums, left, mid)
mergeSort(nums, mid + 1, right)
merge(nums, left, mid, right)
return nums
def reverse(nums, start, end):
i = start
j = end - 1
while i < j:
tmp = nums[i]
nums[i] = nums[j]
nums[j] = tmp
i += 1
j -= 1
def exchange(nums, start, end, index):
reverse(nums, start, index)
reverse(nums, index, end)
reverse(nums, start, end)
def merge(nums, left, mid, right):
i = left
j = mid + 1
while i < j and j <= right:
step = 0
while i < j and nums[i] <= nums[j]:
i += 1
while i < j and j <= right and nums[j] <= nums[i]:
j += 1
step += 1
exchange(nums, i, j, j - step)
i += step
归并排序的链表实现 有几个细节:找到中间的节点可以用快慢表的方法,但是注意此处需要增加 fast.next.next !=None, 否则在1->2这种节点的时候会出现循环不停止, 还有一个细节是左边的和右边递归的时候,需要断开。
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def sortList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head is None or head.next is None:
return head
slow = head
fast = head
##注意1
while fast and fast.next and fast.next.next:
fast = fast.next.next
slow = slow.next
mid_next = slow.next
slow.next = None ##注意2
left = self.sortList(head)
right = self.sortList(mid_next)
res = self.merge(left, right)
return res
def merge(self, left, right):
dummy = ListNode(0)
temp = dummy
while left and right:
if left.val <= right.val:
temp.next = left
left = left.next
temp = temp.next
else:
temp.next = right
right = right.next
temp = temp.next
if left != None:
temp.next = left
if right != None:
temp.next = right
return dummy.next
快速排序
import java.util.Arrays;
public class QuickSort {
private void quickSort(int[] array) {
subQuickSort(array, 0, array.length-1);
}
private void subQuickSort(int[] array, int start, int end) {
if(start >= end) return;
int middleIndex = subQuickSortCore(array, start, end);
subQuickSort(array, start, middleIndex-1);
subQuickSort(array, middleIndex + 1, end);
}
private int subQuickSortCore(int[] array, int start, int end) {
int middleValue = array[start];
while(start < end) {
while(array[end] >= middleValue && start < end) {
end --;
}
array[start] = array[end];
while(array[start] <= middleValue && start < end) {
start ++;
}
array[end] = array[start];
}
array[start] = middleValue;
return start;
}
public static void main(String[] args) {
QuickSort s = new QuickSort();
int [] arrays = new int[] {1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19};
s.quickSort(arrays);
System.out.println(Arrays.toString(arrays));
}
}
非递归实现,可以用栈来实现 (如果题目要求不能开辟新的空间,那么则需要递归求解)
def sort_helper(nums, left, right):
if left > right:
return
pivot = nums[left]
while left < right:
while left < right and nums[left] >= pivot:
right -= 1
nums[left] = nums[right]
while left < right and nums[left] <= pivot:
left += 1
nums[right] = nums[left]
nums[left] = pivot
return left
def nonRecursiveQuickSort(nums):
stack = []
left = 0
right = len(nums) -1
stack.append(left)
stack.append(right)
while len(stack) > 0:
right = stack.pop()
left = stack.pop()
if left >= right:
continue
mid = sort_helper(nums, left, right)
if mid + 1 < right:
stack.append(mid+1)
stack.append(right)
if mid -1 > left:
stack.append(left)
stack.append(mid -1)
链表的快速排序
链表的快速排序,由于链表不能支持从后往前的遍历,所以不能像数组一样实现,但是链表能够实现快速的插入。在lintcode上提交时,需要考虑子链表都相等的情况。
"""
Definition of ListNode
class ListNode(object):
def __init__(self, val, next=None):
self.val = val
self.next = next
"""
class Solution(object):
"""
@param head: The head of linked list.
@return: You should return the head of the sorted linked list, using constant space complexity.
"""
## quickSort
def sortList(self, head):
# write your code here
if head is None or head.next is None:
return head
if self.isduplication(head):
return head
lroot = ListNode(0)
rroot = ListNode(0)
rr = rroot
ll = lroot
pivot = head
head = head.next
while head != None:
if head.val >pivot.val:
rr.next = head
head = head.next
rr = rr.next
rr.next = None
else:
ll.next = head
head = head.next
ll = ll.next
ll.next = None
lp = self.sortList(lroot.next)
rp = self.sortList(rroot.next)
ltemp = lp
while lp != None and lp.next != None:
lp = lp.next
if ltemp != None:
lp.next = pivot
pivot.next = rp
return ltemp
else:
pivot.next = rp
return pivot
def isduplication(self, head):
if head == None or head.next == None:
return True
val = head.val
head = head.next
while head != None:
if head.val == val:
head = head.next
else:
return False
return True
堆排序
二叉堆是一个完全二叉树或者是近似完全二叉树。满足两父节点的特性:父节点的键值总是大于或者等于(小于或者等于)任何一个子节点的键值。每个节点的左右子树都是一个堆
class heapSort(object):
def sort(self, nums):
if nums == None or len(nums) == 0:
return
length = len(nums)
## initialize the heap time complex O(n)
for i in range(length//2-1, -1, -1):
self.adjustHeap(nums, i, length)
## change with the last element time complex O(nlogn)
for i in range(length-1, -1, -1):
tmp = nums[0]
nums[0] = nums[i]
nums[i] = tmp
self.adjustHeap(nums, 0, i)
def adjustHeap(self, nums, index, length):
"""
argv:
nums: the array to sort
index: the non leaf index
length: the length of array to sort
"""
i = 2 * index + 1 ## first child
temp = nums[index]
while i < length:
if i + 1 < length and nums[i+1] > nums[i]:
i = i + 1
if nums[i] < temp:
break
nums[index] = nums[i]
index = i
i = 2 * index + 1
nums[index] = temp
def test():
nums = [1, 4 ,2, 6, 8 ,9 ,14, 0]
solution = heapSort()
print (nums)
solution.sort(nums)
print (nums)
if __name__ == "__main__":
test()
堆实现topk
# -*-- coding:utf-8 -*--
class MinHeap(object):
def __init__(self, x):
self.build(x)
def build(self, x):
if x == None or len(x) == 0:
return
self.data = x
length = len(x)
for i in range(length//2 -1, -1, -1):
self.adjustHeap(i, length)
def adjustHeap(self, index, length):
temp = self.data[index]
i = index * 2 + 1
while i < length:
if i + 1 < length and self.data[i+1] < self.data[i]:
i = i + 1
if temp < self.data[i]:
break
self.data[index] = self.data[i]
index = i
i = 2 * i + 1
self.data[index] = temp
def topK(nums, k):
if k >=len(nums):
return nums
temp = []
for i in range(k):
temp.append(nums[i])
heap = MinHeap(temp)
for i in range(k, len(nums)):
if heap.data[0] >= nums[i]:
continue
else:
heap.data[0] = nums[i]
heap.adjustHeap(0, k)
return heap.data
if __name__ == '__main__':
nums = [3, 12, 4, 9, 10, 0, 5]
print topK(nums, 5)
建堆的时间复杂度分析 它的解是
选择排序
选择排序(升序)每次选择最小的一个,需要进行n次排序
import java.util.Arrays;
public class SelectionSort {
private void selectSort(int[] arrays) {
for(int i=0;i<arrays.length;i++) {
int k = i;
for(int j=i + 1;j<arrays.length; j++) {
if(arrays[j] < arrays[k]) {
k = j;
}
}
if(i != k) {
int temp = arrays[i];
arrays[i] = arrays[k];
arrays[k] = temp;
}
}
}
public static void main(String[] args) {
SelectionSort s = new SelectionSort();
int [] arrays = new int[] {1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19};
s.selectSort(arrays);
System.out.println(Arrays.toString(arrays));
}
}
冒泡排序
比较两个相邻的元素,将值大的放到最后端,这样值大的会一直沉在下面。
import java.util.Arrays;
public class BubbleSort {
private void sort(int [] arrays) {
for(int i = 0;i<arrays.length-1; i++) {
for(int j=0; j < arrays.length - 1 - i; j++) {
if(arrays[j] > arrays[j+1]) {
int temp = arrays[j];
arrays[j] = arrays[j+1];
arrays[j+1] = temp;
}
}
}
}
public static void main(String[] args) {
BubbleSort s = new BubbleSort();
int [] arrays = new int[] {1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19};
s.sort(arrays);
System.out.println(Arrays.toString(arrays));
}
}
插入排序
每次将新元素插入到前面已排序好的子列表中。
import java.util.Arrays;
public class InsertSort {
public void sort(int[] arrays) {
for(int i=1;i<arrays.length;i++) {
int j = i;
int target = arrays[i];
while(j>0 && target < arrays[j-1]) {
arrays[j] = arrays[j-1];
j --;
}
arrays[j] = target;
}
}
public static void main(String[] args) {
InsertSort s = new InsertSort();
int [] arrays = new int[] {1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 17, 17, 177, 18, 8, 8, 19};
s.sort(arrays);
System.out.println(Arrays.toString(arrays));
}
}
拓扑排序
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列,该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次
- 若存在一条从顶点A到顶点B的路径,那么在序列中顶点A出现在顶点B的前面。
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
拓扑排序常用的方法:
- 从DAG图中选择一个没有前驱(即入度为0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边
-
重复上述两个步骤直到DAG图为空或当前图中不存在无前驱的顶点为止。
# --*- coding:utf-8 -*-- def topological_sorting(graph): n = len(graph) indegree = [0 for _ in range(n)] for i in range(n): for j in range(n): if graph[i][j]: indegree[j] += 1 queue = [] for i in range(n): if indegree[i] == 0: queue.append(i) result = [] while len(queue) > 0: node = queue.pop(0) result.append(node) for i in range(n): if graph[node][i]: indegree[i] -= 1 if indegree[i] == 0: queue.append(i) if len(result) == n: return result ## 不存在拓扑排序 else: return [] if __name__ == '__main__': graph = [[0 for _ in range(5)] for _ in range(5)] graph[0][1] = 1 graph[1] [2] = 1 graph[2][4] = 1 graph[0][3] = 1 graph[3][2] = 1 graph[3][4] = 1 graph[0][3] = 1 result = topological_sorting(graph) print result
树的遍历
树的遍历的递归写法都比较简单,可参考以下代码:
ArrayList<Integer> result = new ArrayList<Integer>();
public ArrayList<Integer> postorderTraversal(TreeNode root) {
traversal(root);
return result;
}
public void traversal(TreeNode root) {
if (root == null) {
return ;
}
traversal(root.left);
traversal(root.right);
result.add(root.val);
}
以下均考虑非递归算法
先序遍历
采用辅助栈,每一次弹出一个元素,且注意先将右孩子进栈,再将左孩子进站。
public ArrayList<Integer> preorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<TreeNode>();
ArrayList<Integer> result = new ArrayList<Integer>();
if (root == null) {
return result;
}
stack.push(root);
while(!stack.isEmpty()) {
TreeNode top = stack.pop();
result.add(top.val);
if(top.right != null) {
stack.push(top.right);
}
if(top.left != null) {
stack.push(top.left);
}
}
return result;
}
中序遍历
若节点P的左孩子不为空,需要将当前节点入栈,设左孩子为当前节点。若P的左孩子为空,则输出当前节点,并且设右孩子为当前节点。
public ArrayList<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<TreeNode>();
ArrayList<Integer> result = new ArrayList<Integer>();
while(root != null || !stack.isEmpty()) {
if (root != null) {
stack.add(root);
root = root.left;
}else {
root = stack.pop();
result.add(root.val);
root = root.right;
}
}
return result;
}
后序遍历
后序遍历时当节点不存在左孩子和右孩子,或者存在但均已输出时才可被输出。有一个技巧,将出栈的节点标记为上一个输出的节点,当前栈顶节点设置为当前节点,如此能够快速知道左右结点是否输出。
public ArrayList<Integer> postorderTraversal(TreeNode root){
Stack<TreeNode> stack = new Stack<TreeNode>();
ArrayList<Integer> result = new ArrayList<Integer>();
if (root == null) {
return result;
}
stack.push(root);
TreeNode cur = null;
TreeNode pre = null; // 前一次访问的节点
while(!stack.isEmpty()) {
cur = stack.peek();
// 在后续遍历中 只有当前节点的孩子为空 或者是他的左右节点都访问过的时候 ,才可以被访问
if((cur.left == null && cur.right == null) ||(pre!= null && (pre == cur.left || pre==cur.right))) {
result.add(cur.val);
stack.pop();
pre = cur;
}
else {
if(cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
return result;
}
一个小问题是:任意给两种方式都能还原这颗树吗?
图算法
单源最短路径
Bellman-Fords算法是一种基于计算带权有向图中单源最短路径。对于带权有向图G=(V,E),Dijkstra算法要求G中的边的权值均为非负,而Bellman-Ford算法能够允许存在负边的情况。Bellman-Fords算法采用动态规划(Dynamic Programming)进行设计,实现的时间复杂度为O(V*E),其中V为顶点的数量,E为边的数量。算法描述如下:
- 创建源顶点v到图中所有顶点的距离的集合distSet,为图中的所有顶点指定一个距离值,初始值均为Infinite, 源顶点距离为0;
- 计算最短路径,执行V-1次遍历:对于图中的每条边:对于图中的每条边:如果起点 u 的距离 d 加上边的权值 w 小于终点 v 的距离 d,则更新终点 v 的距离值 d;
-
检测是否存在负环路,即权值只和小于0的环路。对于每一条边,如果存在Distance(u) + w(u,v) < Distance(v)的边,则存在
## -*-- coding:utf-8 -*-- class Edge(object): def __init__(self, u, v, weight): self.u = u self.v = v self.weight = weight def bellman_ford(nodenum, edges, source): MAXINT = 99999 dist = [MAXINT for _ in range(nodenum)] dist[source] = 0 ## 时间复杂度是O(VE) 外层循环 V-1就行 for i in range(nodenum-1): for j in range(len(edges)): if dist[edges[j].u] + edges[j].weight < dist[edges[j].v]: dist[edges[j].v] = dist[edges[j].u] + edges[j].weight ## 判断是否有负环路 flag = True for j in range(len(edges)): if dist[edges[j].u] + edges[j].weight < dist[edges[j].v]: flag = False break if not flag: return dist DijKstra算法是经典的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。时间复杂度是O(2*|E| + |V|^2),采用优先队列后,时间复杂度降为O(2*|E| + |V|log|V|) # -*-- coding:utf-8 -*-- import heapq ## 采用优先队列 def dijkstra(source, n_node, graph): priority_queue = [] priority_queue.append((0, source)) heapq.heapify(priority_queue) MAX_INT = 1000000 dis = [MAX_INT for _ in range(n_node)] dis[source] = 0 while len(priority_queue) > 0: node = heapq.heappop(priority_queue) idx = node[1] for i in range(n_node): if graph[idx][i] != -1: if dis[i] > dis[idx] + graph[idx][i]: dis[i] = dis[idx] + graph[idx][i] heapq.heappush(priority_queue, (dis[i], i)) return dis if __name__ == '__main__': graph_list = [[0, 2, 1, 4, 5, 1], [1, 0, 4, 2, 3, 4], [2, 1, 0, 1, 2, 4], [3, 5, 2, 0, 3, 3], [2, 4, 3, 4, 0, 1], [3, 4, 7, 3, 1, 0]] dis = dijkstra(0, 6, graph_list) print dis
### 最小生成树
prim算法 根据顶点选择 Kruskra算法 根据边选择
动态规划
关于动态规划可以优化空间的总结:实践过程中发现,如果动态规划的转移方程如果只和前一个状态有关,那么空间可以优化,方法为将第二维逆序遍历。原理是说逆序的时候,在下一轮迭代不会更新其前面的值。